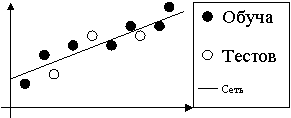Выбор параметров сети.

Это очень важный этап в применении МНСПР. От него зависит будет ли решена задача или нет. В настоящее время нет никаких жестких правил ни для выбора количества скрытых слоев, ни для выбора количества нейронов в них. Хотя существуют ограничения, помогающие принимать решения.

Количество слоев.

1)         Если функция определена на конечном множестве точек, то 3-ехслойный перцептрон способен ее апроксимировать.

2)         Если функция непрерывна и определена на компактной области, то 3-ехслойный перцептрон способен ее апроксимировать.

3)         Остальные функции, которым могут быть обучены нейронные сети, могут быть апроксимированы 4-ехслойным перцетроном.

Таким образом, теоретически максимальное количество слоев, которое необходимо – четыре, или два скрытых слоя. Хотя при решении реальных задач может использоваться большее количество слоев.

Количество нейронов в скрытых слоях.

Выбор правильного количества нейронов в скрытых слоях является очень важным. Слишком малое количество – и сеть не сможет обучиться. Слишком большое повлечет за собой увеличение времени обучения сети до фактически нереального значения. Также это может привести к переобученности сети (overfitting), проявляющейся в том, что сеть будет прекрасно работать на обучающей выборке, но очень плохо на входных примерах не входящих в нее (см. рис. 2.6).

 

а)	б)
Рисунок 2.6. Пример хорошо обученной а) и переобученной б) сети.

 

Это происходит из-за того, что сеть будет обладать избыточными способностями к обучению и наряду со значительными для данной задачи факторами будет учитывать черты, характерные лишь для данной обучающей выборки.

Однако, существуют эвристические правила выбора количества нейронов в скрытых слоях. Одним из таких правил является правило  геометрической пирамиды (geometric pyramid rule) [10].  По этому правилу число нейронов скрытого слоя в 3-ехслойном перцептроне вычисляетмя по следующей формуле:

 

                                                  ,                                                (2.11)

 

где k – число нейронов в скрытом слое,

n – число нейронов во входном слое;

m –  число нейронов в выходном слое.

Для 4-ехслойного перцептрона число нейронов вычисляется несколько сложнее:

 

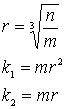                                                                                                            (2.12)   

 

где  - число нейронов в первом скрытом слое;

 - число нейронов во втором скрытом слое.

Хотя существует еще более точный, но и более долгий способ. Он состоит в том, что сначала используется сеть с одним скрытым слоем с одним, двумя нейронами. Если она смогла достигнуть необходимого уровня ошибки, то процесс обучения закончен, иначе добавляем еще один нейрон и так до тех пор, пока ошибка сети не станет приемлемо малой, или до тех пор пока увеличение числа нейронов не сможет значительно улучшить характеристики сети.