Первый период

Все началось в далеком 1942 году. Некто Уоррен Маккалок, нейрофизиолог, изучавший философию и психологию в Йельском университете, а в то время работавший руководителем лаборатории фундаментальных исследований  факультета психиатрии в Иллинойском университете, будучи на  научной конференции в Нью-Йорке, услышал доклад одного из сотрудников Винера  о механизмах обратной связи в биологии. Высказанные в докладе представления об обратной связи в чем-то перекликались с собственными идеями Маккалока относительно работы человеческого мозга. В течение следующего года Маккалок в соавторстве Уолтером Питтсом, который и был тем сотрудником, разработал теорию деятельности головного мозга. Эта теория и явилась той основой, на которой сформировалось широко распространенное мнение, что функции компьютеров и мозга в значительной мере сходны.

Исходя из своих исследований, Маккалок и Питтс [1] выдвинули гипотезу, что нейроны можно упрощенно рассматривать как устройства, оперирующие двоичными числами, получившая впоследствии название «модель нейрона Маккалока-Питтса» :

где,   -  выход нейрона;

- i-ый входной сигнал;

- вес i-ой связи;

 - пороговое значение;

 - количество входных сигналов.

Маккалок и Питтс предложили конструкцию сети из электронных «нейронов» и показали, что подобная сеть может выполнять практически любые вообразимые числовые и логические операции. Далее они предложили, что такая сеть в состоянии также обучаться, распознавать образы, обобщать, т.е. она обладает основными элементами интеллекта.

Эта гипотеза положила начало первому нейрокомпьютерному буму 40-60-х годов. Из этого нейромодельного подхода к машинному разуму сформировался так называемый «восходящий метод» - от простых аналогов нервной системы примитивных существ, обладающих малым числом нейронов, к сложнейшей нервной системе человека и даже выше. Основной трудностью, с которой столкнулся «восходящий метод»  на заре своего существования, была высокая стоимость электронных компонентов. Даже самые совершенные нейронные модели содержали лишь несколько сотен нейронов. Это обстоятельство несколько обескуражило исследователей того времени. Но одним из тех, кто не испугался трудностей, был Фрэнк Розенблатт, молодой ученый-психолог. В середине 1958 г. он продемонстрировал компьютерную модель электронного устройства, названного им перцептроном (от латинского perceptio – понимание, познавание), которое должно было имитировать процессы человеческого мышления.

 Розенблатт запрограммировал один из самых мощных компьютеров того времени IBM-704, так, чтобы тот моделировал действие электронной схемы перцептрона, столь сложной, что мощному компьютеру требовалось около получас на решение задачи, с которой реальный перцептрон, с которой реальный перцептрон должен был справиться за тысячные доли секунды. Перцептрон должен  был передавать сигналы от «глаза», составленного из фотоэлементов, в блоки электромеханических ячеек памяти, которые оценивали относительную величину электрических сигналов. Эти ячейки соединялись между собой случайным образом в соответствии с теорией, согласно которой, мозг воспринимает новую информацию и реагирует на нее через систему случайных связей между нейронами. Таким образом Ф. Розенблатт создал первый программный нейроимитатор искусственной нейронной сети (ИНС) (см. [2]).

В 1960 г. он продемонстрировал перцептрон «Марк-1». Воспринимающим устройством перцептрона служила фотоэлектрическая модель сетчатки – поле рецепторов, состоящее из несколько сотен фотосопротивлений. Каждый элемент поля рецепторов мог находиться в двух состояниях – возбужденном или невозбужденном, в зависимости от того, падает или нет на соответствующее фотосопротивление контур проектируемой на поле фигуры. На выходе каждого элемента появляется сигнал(, где  - число элементов), равный единице, если элемент возбужден, и нулю в противном случае. Следующим слоем перцептрона были так называемые «ассоциативные элементы» или А-элементы. Все они одинаковы; их число (512) было близко к числу рецепторов (400). Каждый из них был нейроном Маккалока Питтса, описываемый формулой (1). Выбор рецепторов, подключаемых к данному А-элементы, так же как и выбор знака подключения, производился случайно (по жребию). Таким образом величина -ой связи  входит в уравнение (1) с минусом, если -ый рецептор подключен к А-элементу со знаком минус, и наоборот. Взвешенная сумма выходных сигналов А-элементов подавалась на вход регулирующего элемента. Если эта сумма была больше или равна нулю, то на выходе персептрона была 1, иначе 0:                                                                         

 

                            

 

Таким образом, перцептрон обладал способностью различать два различных образа.

Функция (2.2), представляющая выход регулирующего элемента, позже получила название пороговой функции (threshold function). Данная функция являлась первой функцией активации (характеристической функцией) нейрона (activation function или transfer function). Позже было предложено большое количество различных видов активационной функции нейрона. Эти функции будут рассмотрены ниже, в разделе относящемся к многослойным нейронным сетям.

Это достижение ободрило многих исследователей, работавших в то время  в области искусственного интеллекта (ИИ). Ученые были полны надежд в  скором времени создать компьютеры на базе перцептронов. Но, весь энтузиазм был омрачен маленьким, но очень досадным недостатком. Перцептрон не мог обучиться функции XOR (исключающее или). Таким образом, было невозможно создать компьютер на искусственных нейронах, так как он не мог вычислить функцию XOR, потому что эта функция линейно не разделима. Марвин Минский и Сеймур Пейперт доказали это математически в своей книге «Перцептроны» [3] (1969). «Исключающее или» функция от двух аргументов, каждый из которых может быть нулем или единицей. Она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рис. 1.

 

Рисунок 2.1. Однонейронная система с двумя входами.

 

Обозначим один вход через , а другой через . Веса входов  и  соответственно. Тогда все их возможные комбинации будут состоять из четырех точек на плоскости x-у, как показано на рис.2.1.

 

 

 

Рисунок  2.2. Представление выходов однонейронной системы на плоскости.

 

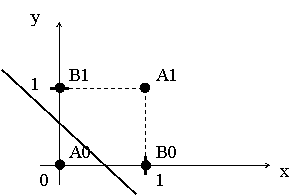
Например, точка х=0 и у=0 обозначена на рисунке как точка А0.

В табл. 2.1 представлена таблица истинности для функции «ИСКЛЮЧАЮЩЕЕ ИЛИ». Значения функции равные нулю помечены А0 и А1, равные единице - В0 и В1.

 

Таблица 2.1. Таблица истинности для функции «Исключающее ИЛИ».

Точка	Значение входа X	Значение входа Y	Значение на выходе
А0	0	0	0
В0	1	0	1
В1	0	1	1
А1	1	1	0

 

В сети на рис.2.1. функция  является пороговой функцией (2).

Примем следующее обозначение:

 

                                        

 

В англоязычной литературе взвешенная сумма входов называется net input.

Чтобы понять это ограничение, зафиксируем  на величине порога 0,5. Уравнение (2.3) линейно по x и у, т.е. все значения по х и у, удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости х-у. Любые входные значения для х и у на этой линии будут давать пороговое значение 0,5 для . Входные значения с одной стороны прямой обеспечат значения  больше порога, следовательно, =1. Входные значения по другую сторону прямой обеспечат значения  меньше порогового значения, делая  равным 0. Изменения значений ,   и порога будут менять наклон и положение прямой. Для того чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ,  заданную табл.2.1, нужно расположить прямую так, чтобы точки А были с одной стороны прямой, а точки В - с другой. Попытавшись нарисовать такую прямую на рис.2.2, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции ИСКЛЮЧАЮЩЕЕ ИЛИ.

Как видно из всего вышесказанного, невозможно нарисовать прямую линию, разделяющую плоскость х-у так, чтобы реализовывалась функция «ИСКЛЮЧАЮЩЕЕ ИЛИ». Этот пример не единственный. Имеется обширный класс функций, не реализуемых однослойной сетью. Об этих функциях говорят, что они являются линейно неразделимыми, и они накладывают определенные ограничения на возможности однослойных сетей. Линейная разделимость ограничивает однослойные сети задачами классификации, в которых множества точек (соответствующих входным значениям) могут быть разделены геометрически. Для нашего случая с двумя входами разделитель является прямой линией. В случае трех входов разделение осуществляется плоскостью, рассекающей трехмерное пространство. Для четырех или более входов визуализация невозможна, и необходимо мысленно представить n-мерное пространство, рассекаемое «гиперплоскостью» - геометрическим объектом, который рассекает пространство четырех или большего числа измерений.

К концу 60-х годов проблема линейной разделимости была хорошо понята. К тому же было известно, что это серьезное ограничение представляемости однослойными сетями можно преодолеть, добавив дополнительные слои. Например, двухслойные сети можно получить каскадным соединением двух однослойных сетей. Они способны выполнять более общие классификации, отделяя те точки, которые содержатся в выпуклых ограниченных или неограниченных областях.

Несмотря на то, что возможности многослойных сетей были известны давно, в течение многих лет не было теоретически обоснованного алгоритма для настройки их весов.

Таким образом, книга Минского и Пейперта ознаменовала собой конец первого периода интереса к искусственным нейронным сетям.